
前言
A*算法要解决的问题是找出一条起点到终点的最优路径,本文主要演示使用js代码实现的方法。讨论A*算法原理的优质文章很多,我会在下面附上相关文章链接,不文不再详细讨论原理。在后面的文章中我将用Cesium结合A*实现依照地形的路径规划。
算法核心
A*算法的核心在于它通过代价f来决定下一个要探索的节点。g为历史代价,从起始到当前节点的实际成本;h为预期代价,从当前节点到终点的估计成本。
计算过程
- 将起点加入开放列表(openList),这是一个待处理节点的集合。
- 重复以下过程直到开放列表为空。
- 从开放列表中选择f最小的节点作为当前节点。
- 如果当前节点是终点,则构造路径并结束。
- 否则,遍历当前节点的每一个邻居节点。
- 如果邻居节点已经被关闭,则忽略它。
- 反之,则计算它的f值,设置当前节点为它的父节点,并将其加入开放列表。
- 如果邻居节点已经被计算过f值,则检查通过当前节点到达该邻居节点是否提供了一条更短的路径。如果是,则更新它的g值和父节点。
- 将当前关闭并从开放列表移除。
- 如果开放列表为空而没有找到路径,则表示不存在从起点到目标的路径。
在线Demo
1.计算过程演示

2.交互式演示
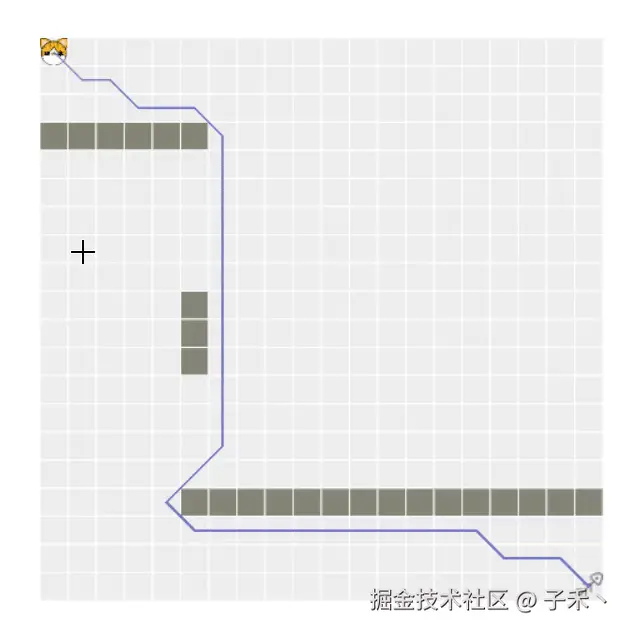
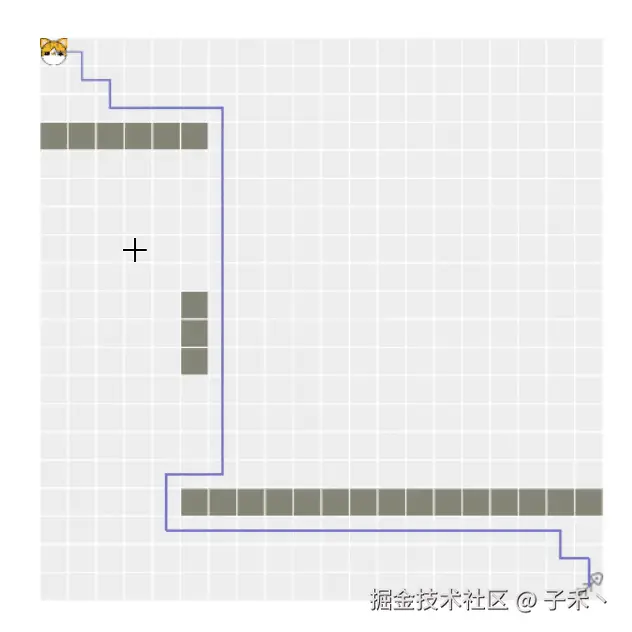
完整代码
下面是直接可以运行且添加了详细注解的代码,可以参照上面的计算过程理解下面的代码。
html
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<meta name="viewport" content="width=device-width, initial-scale=1.0">
<title>Document</title>
<style>
canvas {
margin: 20px;
}
</style>
</head>
<body>
<canvas width="600" height="600"></canvas>
</body>
<script>
let grid = [[{ "x": 0, "y": 0, "id": "0-0" }, { "x": 1, "y": 0, "id": "1-0" }, { "x": 2, "y": 0, "id": "2-0" }, { "x": 3, "y": 0, "id": "3-0" }, { "x": 4, "y": 0, "id": "4-0" }, { "x": 5, "y": 0, "id": "5-0" }, { "x": 6, "y": 0, "id": "6-0" }, { "x": 7, "y": 0, "id": "7-0" }, { "x": 8, "y": 0, "id": "8-0" }, { "x": 9, "y": 0, "id": "9-0" }, { "x": 10, "y": 0, "id": "10-0" }, { "x": 11, "y": 0, "id": "11-0" }, { "x": 12, "y": 0, "id": "12-0" }, { "x": 13, "y": 0, "id": "13-0" }, { "x": 14, "y": 0, "id": "14-0" }, { "x": 15, "y": 0, "id": "15-0" }, { "x": 16, "y": 0, "id": "16-0" }, { "x": 17, "y": 0, "id": "17-0" }, { "x": 18, "y": 0, "id": "18-0" }, { "x": 19, "y": 0, "id": "19-0" }], [{ "x": 0, "y": 1, "id": "0-1" }, { "x": 1, "y": 1, "id": "1-1" }, { "x": 2, "y": 1, "id": "2-1" }, { "x": 3, "y": 1, "id": "3-1" }, { "x": 4, "y": 1, "id": "4-1" }, { "x": 5, "y": 1, "id": "5-1" }, { "x": 6, "y": 1, "id": "6-1" }, { "x": 7, "y": 1, "id": "7-1" }, { "x": 8, "y": 1, "id": "8-1" }, { "x": 9, "y": 1, "id": "9-1" }, { "x": 10, "y": 1, "id": "10-1" }, { "x": 11, "y": 1, "id": "11-1" }, { "x": 12, "y": 1, "id": "12-1" }, { "x": 13, "y": 1, "id": "13-1" }, { "x": 14, "y": 1, "id": "14-1" }, { "x": 15, "y": 1, "id": "15-1" }, { "x": 16, "y": 1, "id": "16-1" }, { "x": 17, "y": 1, "id": "17-1" }, { "x": 18, "y": 1, "id": "18-1" }, { "x": 19, "y": 1, "id": "19-1" }], [{ "x": 0, "y": 2, "id": "0-2" }, { "x": 1, "y": 2, "id": "1-2" }, { "x": 2, "y": 2, "id": "2-2" }, { "x": 3, "y": 2, "id": "3-2" }, { "x": 4, "y": 2, "id": "4-2" }, { "x": 5, "y": 2, "id": "5-2" }, { "x": 6, "y": 2, "id": "6-2" }, { "x": 7, "y": 2, "id": "7-2" }, { "x": 8, "y": 2, "id": "8-2" }, { "x": 9, "y": 2, "id": "9-2" }, { "x": 10, "y": 2, "id": "10-2" }, { "x": 11, "y": 2, "id": "11-2" }, { "x": 12, "y": 2, "id": "12-2" }, { "x": 13, "y": 2, "id": "13-2" }, { "x": 14, "y": 2, "id": "14-2" }, { "x": 15, "y": 2, "id": "15-2" }, { "x": 16, "y": 2, "id": "16-2" }, { "x": 17, "y": 2, "id": "17-2" }, { "x": 18, "y": 2, "id": "18-2" }, { "x": 19, "y": 2, "id": "19-2" }], [{ "x": 0, "y": 3, "id": "0-3", "isClose": true }, { "x": 1, "y": 3, "id": "1-3", "isClose": true }, { "x": 2, "y": 3, "id": "2-3", "isClose": true }, { "x": 3, "y": 3, "id": "3-3", "isClose": true }, { "x": 4, "y": 3, "id": "4-3", "isClose": true }, { "x": 5, "y": 3, "id": "5-3", "isClose": true }, { "x": 6, "y": 3, "id": "6-3" }, { "x": 7, "y": 3, "id": "7-3" }, { "x": 8, "y": 3, "id": "8-3" }, { "x": 9, "y": 3, "id": "9-3" }, { "x": 10, "y": 3, "id": "10-3" }, { "x": 11, "y": 3, "id": "11-3" }, { "x": 12, "y": 3, "id": "12-3" }, { "x": 13, "y": 3, "id": "13-3" }, { "x": 14, "y": 3, "id": "14-3" }, { "x": 15, "y": 3, "id": "15-3" }, { "x": 16, "y": 3, "id": "16-3" }, { "x": 17, "y": 3, "id": "17-3" }, { "x": 18, "y": 3, "id": "18-3" }, { "x": 19, "y": 3, "id": "19-3" }], [{ "x": 0, "y": 4, "id": "0-4" }, { "x": 1, "y": 4, "id": "1-4" }, { "x": 2, "y": 4, "id": "2-4" }, { "x": 3, "y": 4, "id": "3-4" }, { "x": 4, "y": 4, "id": "4-4" }, { "x": 5, "y": 4, "id": "5-4" }, { "x": 6, "y": 4, "id": "6-4" }, { "x": 7, "y": 4, "id": "7-4" }, { "x": 8, "y": 4, "id": "8-4" }, { "x": 9, "y": 4, "id": "9-4" }, { "x": 10, "y": 4, "id": "10-4" }, { "x": 11, "y": 4, "id": "11-4" }, { "x": 12, "y": 4, "id": "12-4" }, { "x": 13, "y": 4, "id": "13-4" }, { "x": 14, "y": 4, "id": "14-4" }, { "x": 15, "y": 4, "id": "15-4" }, { "x": 16, "y": 4, "id": "16-4" }, { "x": 17, "y": 4, "id": "17-4" }, { "x": 18, "y": 4, "id": "18-4" }, { "x": 19, "y": 4, "id": "19-4" }], [{ "x": 0, "y": 5, "id": "0-5" }, { "x": 1, "y": 5, "id": "1-5" }, { "x": 2, "y": 5, "id": "2-5" }, { "x": 3, "y": 5, "id": "3-5" }, { "x": 4, "y": 5, "id": "4-5" }, { "x": 5, "y": 5, "id": "5-5" }, { "x": 6, "y": 5, "id": "6-5" }, { "x": 7, "y": 5, "id": "7-5" }, { "x": 8, "y": 5, "id": "8-5" }, { "x": 9, "y": 5, "id": "9-5" }, { "x": 10, "y": 5, "id": "10-5" }, { "x": 11, "y": 5, "id": "11-5" }, { "x": 12, "y": 5, "id": "12-5" }, { "x": 13, "y": 5, "id": "13-5" }, { "x": 14, "y": 5, "id": "14-5" }, { "x": 15, "y": 5, "id": "15-5" }, { "x": 16, "y": 5, "id": "16-5" }, { "x": 17, "y": 5, "id": "17-5" }, { "x": 18, "y": 5, "id": "18-5" }, { "x": 19, "y": 5, "id": "19-5" }], [{ "x": 0, "y": 6, "id": "0-6" }, { "x": 1, "y": 6, "id": "1-6" }, { "x": 2, "y": 6, "id": "2-6" }, { "x": 3, "y": 6, "id": "3-6" }, { "x": 4, "y": 6, "id": "4-6" }, { "x": 5, "y": 6, "id": "5-6" }, { "x": 6, "y": 6, "id": "6-6" }, { "x": 7, "y": 6, "id": "7-6" }, { "x": 8, "y": 6, "id": "8-6" }, { "x": 9, "y": 6, "id": "9-6" }, { "x": 10, "y": 6, "id": "10-6" }, { "x": 11, "y": 6, "id": "11-6" }, { "x": 12, "y": 6, "id": "12-6" }, { "x": 13, "y": 6, "id": "13-6" }, { "x": 14, "y": 6, "id": "14-6" }, { "x": 15, "y": 6, "id": "15-6" }, { "x": 16, "y": 6, "id": "16-6" }, { "x": 17, "y": 6, "id": "17-6" }, { "x": 18, "y": 6, "id": "18-6" }, { "x": 19, "y": 6, "id": "19-6" }], [{ "x": 0, "y": 7, "id": "0-7" }, { "x": 1, "y": 7, "id": "1-7" }, { "x": 2, "y": 7, "id": "2-7" }, { "x": 3, "y": 7, "id": "3-7" }, { "x": 4, "y": 7, "id": "4-7" }, { "x": 5, "y": 7, "id": "5-7" }, { "x": 6, "y": 7, "id": "6-7" }, { "x": 7, "y": 7, "id": "7-7" }, { "x": 8, "y": 7, "id": "8-7" }, { "x": 9, "y": 7, "id": "9-7" }, { "x": 10, "y": 7, "id": "10-7" }, { "x": 11, "y": 7, "id": "11-7" }, { "x": 12, "y": 7, "id": "12-7" }, { "x": 13, "y": 7, "id": "13-7" }, { "x": 14, "y": 7, "id": "14-7" }, { "x": 15, "y": 7, "id": "15-7" }, { "x": 16, "y": 7, "id": "16-7" }, { "x": 17, "y": 7, "id": "17-7" }, { "x": 18, "y": 7, "id": "18-7" }, { "x": 19, "y": 7, "id": "19-7" }], [{ "x": 0, "y": 8, "id": "0-8" }, { "x": 1, "y": 8, "id": "1-8" }, { "x": 2, "y": 8, "id": "2-8" }, { "x": 3, "y": 8, "id": "3-8" }, { "x": 4, "y": 8, "id": "4-8" }, { "x": 5, "y": 8, "id": "5-8" }, { "x": 6, "y": 8, "id": "6-8" }, { "x": 7, "y": 8, "id": "7-8" }, { "x": 8, "y": 8, "id": "8-8" }, { "x": 9, "y": 8, "id": "9-8" }, { "x": 10, "y": 8, "id": "10-8" }, { "x": 11, "y": 8, "id": "11-8" }, { "x": 12, "y": 8, "id": "12-8" }, { "x": 13, "y": 8, "id": "13-8" }, { "x": 14, "y": 8, "id": "14-8" }, { "x": 15, "y": 8, "id": "15-8" }, { "x": 16, "y": 8, "id": "16-8" }, { "x": 17, "y": 8, "id": "17-8" }, { "x": 18, "y": 8, "id": "18-8" }, { "x": 19, "y": 8, "id": "19-8" }], [{ "x": 0, "y": 9, "id": "0-9" }, { "x": 1, "y": 9, "id": "1-9" }, { "x": 2, "y": 9, "id": "2-9" }, { "x": 3, "y": 9, "id": "3-9" }, { "x": 4, "y": 9, "id": "4-9" }, { "x": 5, "y": 9, "id": "5-9", "isClose": true }, { "x": 6, "y": 9, "id": "6-9" }, { "x": 7, "y": 9, "id": "7-9" }, { "x": 8, "y": 9, "id": "8-9" }, { "x": 9, "y": 9, "id": "9-9" }, { "x": 10, "y": 9, "id": "10-9" }, { "x": 11, "y": 9, "id": "11-9" }, { "x": 12, "y": 9, "id": "12-9" }, { "x": 13, "y": 9, "id": "13-9" }, { "x": 14, "y": 9, "id": "14-9" }, { "x": 15, "y": 9, "id": "15-9" }, { "x": 16, "y": 9, "id": "16-9" }, { "x": 17, "y": 9, "id": "17-9" }, { "x": 18, "y": 9, "id": "18-9" }, { "x": 19, "y": 9, "id": "19-9" }], [{ "x": 0, "y": 10, "id": "0-10" }, { "x": 1, "y": 10, "id": "1-10" }, { "x": 2, "y": 10, "id": "2-10" }, { "x": 3, "y": 10, "id": "3-10" }, { "x": 4, "y": 10, "id": "4-10" }, { "x": 5, "y": 10, "id": "5-10", "isClose": true }, { "x": 6, "y": 10, "id": "6-10" }, { "x": 7, "y": 10, "id": "7-10" }, { "x": 8, "y": 10, "id": "8-10" }, { "x": 9, "y": 10, "id": "9-10" }, { "x": 10, "y": 10, "id": "10-10" }, { "x": 11, "y": 10, "id": "11-10" }, { "x": 12, "y": 10, "id": "12-10" }, { "x": 13, "y": 10, "id": "13-10" }, { "x": 14, "y": 10, "id": "14-10" }, { "x": 15, "y": 10, "id": "15-10" }, { "x": 16, "y": 10, "id": "16-10" }, { "x": 17, "y": 10, "id": "17-10" }, { "x": 18, "y": 10, "id": "18-10" }, { "x": 19, "y": 10, "id": "19-10" }], [{ "x": 0, "y": 11, "id": "0-11" }, { "x": 1, "y": 11, "id": "1-11" }, { "x": 2, "y": 11, "id": "2-11" }, { "x": 3, "y": 11, "id": "3-11" }, { "x": 4, "y": 11, "id": "4-11" }, { "x": 5, "y": 11, "id": "5-11", "isClose": true }, { "x": 6, "y": 11, "id": "6-11" }, { "x": 7, "y": 11, "id": "7-11" }, { "x": 8, "y": 11, "id": "8-11" }, { "x": 9, "y": 11, "id": "9-11" }, { "x": 10, "y": 11, "id": "10-11" }, { "x": 11, "y": 11, "id": "11-11" }, { "x": 12, "y": 11, "id": "12-11" }, { "x": 13, "y": 11, "id": "13-11" }, { "x": 14, "y": 11, "id": "14-11" }, { "x": 15, "y": 11, "id": "15-11" }, { "x": 16, "y": 11, "id": "16-11" }, { "x": 17, "y": 11, "id": "17-11" }, { "x": 18, "y": 11, "id": "18-11" }, { "x": 19, "y": 11, "id": "19-11" }], [{ "x": 0, "y": 12, "id": "0-12" }, { "x": 1, "y": 12, "id": "1-12" }, { "x": 2, "y": 12, "id": "2-12" }, { "x": 3, "y": 12, "id": "3-12" }, { "x": 4, "y": 12, "id": "4-12" }, { "x": 5, "y": 12, "id": "5-12" }, { "x": 6, "y": 12, "id": "6-12" }, { "x": 7, "y": 12, "id": "7-12" }, { "x": 8, "y": 12, "id": "8-12" }, { "x": 9, "y": 12, "id": "9-12" }, { "x": 10, "y": 12, "id": "10-12" }, { "x": 11, "y": 12, "id": "11-12" }, { "x": 12, "y": 12, "id": "12-12" }, { "x": 13, "y": 12, "id": "13-12" }, { "x": 14, "y": 12, "id": "14-12" }, { "x": 15, "y": 12, "id": "15-12" }, { "x": 16, "y": 12, "id": "16-12" }, { "x": 17, "y": 12, "id": "17-12" }, { "x": 18, "y": 12, "id": "18-12" }, { "x": 19, "y": 12, "id": "19-12" }], [{ "x": 0, "y": 13, "id": "0-13" }, { "x": 1, "y": 13, "id": "1-13" }, { "x": 2, "y": 13, "id": "2-13" }, { "x": 3, "y": 13, "id": "3-13" }, { "x": 4, "y": 13, "id": "4-13" }, { "x": 5, "y": 13, "id": "5-13" }, { "x": 6, "y": 13, "id": "6-13" }, { "x": 7, "y": 13, "id": "7-13" }, { "x": 8, "y": 13, "id": "8-13" }, { "x": 9, "y": 13, "id": "9-13" }, { "x": 10, "y": 13, "id": "10-13" }, { "x": 11, "y": 13, "id": "11-13" }, { "x": 12, "y": 13, "id": "12-13" }, { "x": 13, "y": 13, "id": "13-13" }, { "x": 14, "y": 13, "id": "14-13" }, { "x": 15, "y": 13, "id": "15-13" }, { "x": 16, "y": 13, "id": "16-13" }, { "x": 17, "y": 13, "id": "17-13" }, { "x": 18, "y": 13, "id": "18-13" }, { "x": 19, "y": 13, "id": "19-13" }], [{ "x": 0, "y": 14, "id": "0-14" }, { "x": 1, "y": 14, "id": "1-14" }, { "x": 2, "y": 14, "id": "2-14" }, { "x": 3, "y": 14, "id": "3-14" }, { "x": 4, "y": 14, "id": "4-14" }, { "x": 5, "y": 14, "id": "5-14" }, { "x": 6, "y": 14, "id": "6-14" }, { "x": 7, "y": 14, "id": "7-14" }, { "x": 8, "y": 14, "id": "8-14" }, { "x": 9, "y": 14, "id": "9-14" }, { "x": 10, "y": 14, "id": "10-14" }, { "x": 11, "y": 14, "id": "11-14" }, { "x": 12, "y": 14, "id": "12-14" }, { "x": 13, "y": 14, "id": "13-14" }, { "x": 14, "y": 14, "id": "14-14" }, { "x": 15, "y": 14, "id": "15-14" }, { "x": 16, "y": 14, "id": "16-14" }, { "x": 17, "y": 14, "id": "17-14" }, { "x": 18, "y": 14, "id": "18-14" }, { "x": 19, "y": 14, "id": "19-14" }], [{ "x": 0, "y": 15, "id": "0-15" }, { "x": 1, "y": 15, "id": "1-15" }, { "x": 2, "y": 15, "id": "2-15" }, { "x": 3, "y": 15, "id": "3-15" }, { "x": 4, "y": 15, "id": "4-15" }, { "x": 5, "y": 15, "id": "5-15" }, { "x": 6, "y": 15, "id": "6-15" }, { "x": 7, "y": 15, "id": "7-15" }, { "x": 8, "y": 15, "id": "8-15" }, { "x": 9, "y": 15, "id": "9-15" }, { "x": 10, "y": 15, "id": "10-15" }, { "x": 11, "y": 15, "id": "11-15" }, { "x": 12, "y": 15, "id": "12-15" }, { "x": 13, "y": 15, "id": "13-15" }, { "x": 14, "y": 15, "id": "14-15" }, { "x": 15, "y": 15, "id": "15-15" }, { "x": 16, "y": 15, "id": "16-15" }, { "x": 17, "y": 15, "id": "17-15" }, { "x": 18, "y": 15, "id": "18-15" }, { "x": 19, "y": 15, "id": "19-15" }], [{ "x": 0, "y": 16, "id": "0-16" }, { "x": 1, "y": 16, "id": "1-16" }, { "x": 2, "y": 16, "id": "2-16" }, { "x": 3, "y": 16, "id": "3-16" }, { "x": 4, "y": 16, "id": "4-16" }, { "x": 5, "y": 16, "id": "5-16", "isClose": true }, { "x": 6, "y": 16, "id": "6-16", "isClose": true }, { "x": 7, "y": 16, "id": "7-16", "isClose": true }, { "x": 8, "y": 16, "id": "8-16", "isClose": true }, { "x": 9, "y": 16, "id": "9-16", "isClose": true }, { "x": 10, "y": 16, "id": "10-16", "isClose": true }, { "x": 11, "y": 16, "id": "11-16", "isClose": true }, { "x": 12, "y": 16, "id": "12-16", "isClose": true }, { "x": 13, "y": 16, "id": "13-16", "isClose": true }, { "x": 14, "y": 16, "id": "14-16", "isClose": true }, { "x": 15, "y": 16, "id": "15-16", "isClose": true }, { "x": 16, "y": 16, "id": "16-16", "isClose": true }, { "x": 17, "y": 16, "id": "17-16", "isClose": true }, { "x": 18, "y": 16, "id": "18-16", "isClose": true }, { "x": 19, "y": 16, "id": "19-16", "isClose": true }], [{ "x": 0, "y": 17, "id": "0-17" }, { "x": 1, "y": 17, "id": "1-17" }, { "x": 2, "y": 17, "id": "2-17" }, { "x": 3, "y": 17, "id": "3-17" }, { "x": 4, "y": 17, "id": "4-17" }, { "x": 5, "y": 17, "id": "5-17" }, { "x": 6, "y": 17, "id": "6-17" }, { "x": 7, "y": 17, "id": "7-17" }, { "x": 8, "y": 17, "id": "8-17" }, { "x": 9, "y": 17, "id": "9-17" }, { "x": 10, "y": 17, "id": "10-17" }, { "x": 11, "y": 17, "id": "11-17" }, { "x": 12, "y": 17, "id": "12-17" }, { "x": 13, "y": 17, "id": "13-17" }, { "x": 14, "y": 17, "id": "14-17" }, { "x": 15, "y": 17, "id": "15-17" }, { "x": 16, "y": 17, "id": "16-17" }, { "x": 17, "y": 17, "id": "17-17" }, { "x": 18, "y": 17, "id": "18-17" }, { "x": 19, "y": 17, "id": "19-17" }], [{ "x": 0, "y": 18, "id": "0-18" }, { "x": 1, "y": 18, "id": "1-18" }, { "x": 2, "y": 18, "id": "2-18" }, { "x": 3, "y": 18, "id": "3-18" }, { "x": 4, "y": 18, "id": "4-18" }, { "x": 5, "y": 18, "id": "5-18" }, { "x": 6, "y": 18, "id": "6-18" }, { "x": 7, "y": 18, "id": "7-18" }, { "x": 8, "y": 18, "id": "8-18" }, { "x": 9, "y": 18, "id": "9-18" }, { "x": 10, "y": 18, "id": "10-18" }, { "x": 11, "y": 18, "id": "11-18" }, { "x": 12, "y": 18, "id": "12-18" }, { "x": 13, "y": 18, "id": "13-18" }, { "x": 14, "y": 18, "id": "14-18" }, { "x": 15, "y": 18, "id": "15-18" }, { "x": 16, "y": 18, "id": "16-18" }, { "x": 17, "y": 18, "id": "17-18" }, { "x": 18, "y": 18, "id": "18-18" }, { "x": 19, "y": 18, "id": "19-18" }], [{ "x": 0, "y": 19, "id": "0-19" }, { "x": 1, "y": 19, "id": "1-19" }, { "x": 2, "y": 19, "id": "2-19" }, { "x": 3, "y": 19, "id": "3-19" }, { "x": 4, "y": 19, "id": "4-19" }, { "x": 5, "y": 19, "id": "5-19" }, { "x": 6, "y": 19, "id": "6-19" }, { "x": 7, "y": 19, "id": "7-19" }, { "x": 8, "y": 19, "id": "8-19" }, { "x": 9, "y": 19, "id": "9-19" }, { "x": 10, "y": 19, "id": "10-19" }, { "x": 11, "y": 19, "id": "11-19" }, { "x": 12, "y": 19, "id": "12-19" }, { "x": 13, "y": 19, "id": "13-19" }, { "x": 14, "y": 19, "id": "14-19" }, { "x": 15, "y": 19, "id": "15-19" }, { "x": 16, "y": 19, "id": "16-19" }, { "x": 17, "y": 19, "id": "17-19" }, { "x": 18, "y": 19, "id": "18-19" }, { "x": 19, "y": 19, "id": "19-19" }]]
let origin = grid[0][0];//定义起点
let destination = grid[19][19];//定义终点
let canvas = document.querySelector("canvas");
let ctx = canvas.getContext("2d");
//在canvas上绘制网格,并为grid数组中的每一项添加boundingClientRect(left,top,width,height)属性和h属性(预期代价)
for (let i = 0; i < grid.length; i++) {
for (let j = 0; j < grid[i].length; j++) {
ctx.beginPath();
let node = grid[i][j];
let width = canvas.width / grid[i].length;
let height = canvas.height / grid.length;
if (node.isClose) {
ctx.fillStyle = "#868679";
} else {
ctx.fillStyle = "#eee";
}
let left = node.x * width;
let top = node.y * height;
ctx.rect(left, top, width, height);
node.boundingClientRect = {
left,
top,
width,
height
};
ctx.fill();
ctx.strokeStyle = "#fff";
ctx.lineWidth = 1;
ctx.stroke();
if (origin.id == node.id) {
let img = new Image();
img.src = "./images/origin.png";
img.onload = function () {
ctx.drawImage(img, left, top, width, height);
}
} else if (destination.id == node.id) {
let img = new Image();
img.src = "./images/destination.png";
img.onload = function () {
ctx.drawImage(img, left, top, width, height);
}
}
//计算每个节点的预期代价(与终点的距离)
node.h = Math.sqrt(Math.pow(j - destination.x, 2) + Math.pow(i - destination.y, 2));
}
}
let openList = [];//待计算的节点
origin.g = 0;//初始化起点的历史代价
openList.push(origin);
while (openList.length) {
//根据代价逆序排序,从openList中获取到代价最小的节点(如果有多个代价相同的点,优先选择 g 值(历史代价)较小的节点,这更有可能导向最短路径。)
let sortedByF = openList.sort((a, b) => {
if (a.f == b.f) {
return a.g - b.g;
}
return a.f - b.f
});
//将代价最小的节点设置为当前要计算节点
let nodeCurrent = sortedByF[0];
//如果当前节点是终点,构造路径并结束
if (nodeCurrent.id == destination.id) {
ctx.beginPath();
let parentId = destination.parentId;
ctx.moveTo(destination.boundingClientRect.left + destination.boundingClientRect.width / 2, destination.boundingClientRect.top + destination.boundingClientRect.height / 2);
//根据parentId一层层回溯出最短路径
while (parentId) {
let lastNode = grid.flat().find(({ id }) => id == parentId);
ctx.strokeStyle = "#6c76ca";
ctx.lineTo(lastNode.boundingClientRect.left + lastNode.boundingClientRect.width / 2, lastNode.boundingClientRect.top + lastNode.boundingClientRect.height / 2);
ctx.stroke();
parentId = lastNode.parentId;
}
break;
}
//获取当前节点周围的节点
let childUp = grid[nodeCurrent.y - 1]?.[nodeCurrent.x];//上
let childRight = grid[nodeCurrent.y]?.[nodeCurrent.x + 1];//下
let childDown = grid[nodeCurrent.y + 1]?.[nodeCurrent.x];//左
let childLeft = grid[nodeCurrent.y]?.[nodeCurrent.x - 1];//右边
let childList = [childUp, childRight, childDown, childLeft];
//只有当左边和上边不全是障碍物,才能走左上的节点
if (!childUp?.isClose || !childLeft?.isClose) {
let childLeftUp = grid[nodeCurrent.y - 1]?.[nodeCurrent.x - 1];
childList.push(childLeftUp);
}
//只有当右边和上边不全是障碍物,才能走右上的节点
if (!childUp?.isClose || !childRight?.isClose) {
let childRightUp = grid[nodeCurrent.y - 1]?.[nodeCurrent.x + 1];
childList.push(childRightUp);
}
//只有当右边和下边不全是障碍物,才能走右下的节点
if (!childDown?.isClose || !childRight?.isClose) {
let childRightDown = grid[nodeCurrent.y + 1]?.[nodeCurrent.x + 1];
childList.push(childRightDown);
}
//只有当左边和下边不全是障碍物,才能走左下的节点
if (!childDown?.isClose || !childLeft?.isClose) {
let childLeftDown = grid[nodeCurrent.y + 1]?.[nodeCurrent.x - 1];
childList.push(childLeftDown);
}
//为周围的节点设置父节点id
for (let i = 0; i < childList.length; i++) {
let child = childList[i];
if (!child || child.isClose) {//child.isClose代表已经关闭或为障碍,不计算
continue
}
//计算当前节点到它子节点的距离
let currentToChild = Math.sqrt(Math.pow(nodeCurrent.x - child.x, 2) + Math.pow(nodeCurrent.y - child.y, 2));
if (child.f === undefined) {//这个子节点的代价从来没有被计算过,现在计算它的代价
child.parentId = nodeCurrent.id;
//子节点的历史代价是当前节点历史代价加上当前节点到子节点的距离
child.g = nodeCurrent.g + currentToChild;
//子节点的未来期望代价是子节点到终点的距离
child.h = Math.sqrt(Math.pow(child.x - destination.x, 2) + Math.pow(child.y - destination.y, 2));
//得出最终代价
child.f = child.g + child.h;
openList.push(child);//将这个子节点加入到待计算列表中
} else {//这个子节点被计算过
// 将子节点的父级替换为当前节点重新计算历史代价
let g = nodeCurrent.g + currentToChild;
//如果更换为新父级后历史代价比以前小,就更新它的父节点为当前节点
if (g < child.g) {
child.g = g;
child.f = child.g + child.h;
child.parentId = nodeCurrent.id;
}
}
}
//将当前节点从待计算列表中移除并将它关闭
let index = openList.findIndex(({ id }) => id == nodeCurrent.id);
openList[index].isClose = true;
openList.splice(index, 1);
}
</script>
</html>